Viscous fluid conduit
My research centers on wave dynamics in a two-Stokes viscous core-annular flow system, or conduit model, which I use as an experimental and theoretical framework for studying wave propagation in simplified geophysical settings, including magma and sub-glacier water channels. This system, featuring a buoyancy-driven Stokes core fluid surrounded by a heavier, miscible Stokes fluid, allows for controlled investigations into boundary-forced wave generation mechanisms. The wave dynamics are governed by the conduit equation that represents the normalized, axisymmetric cross-sectional area.

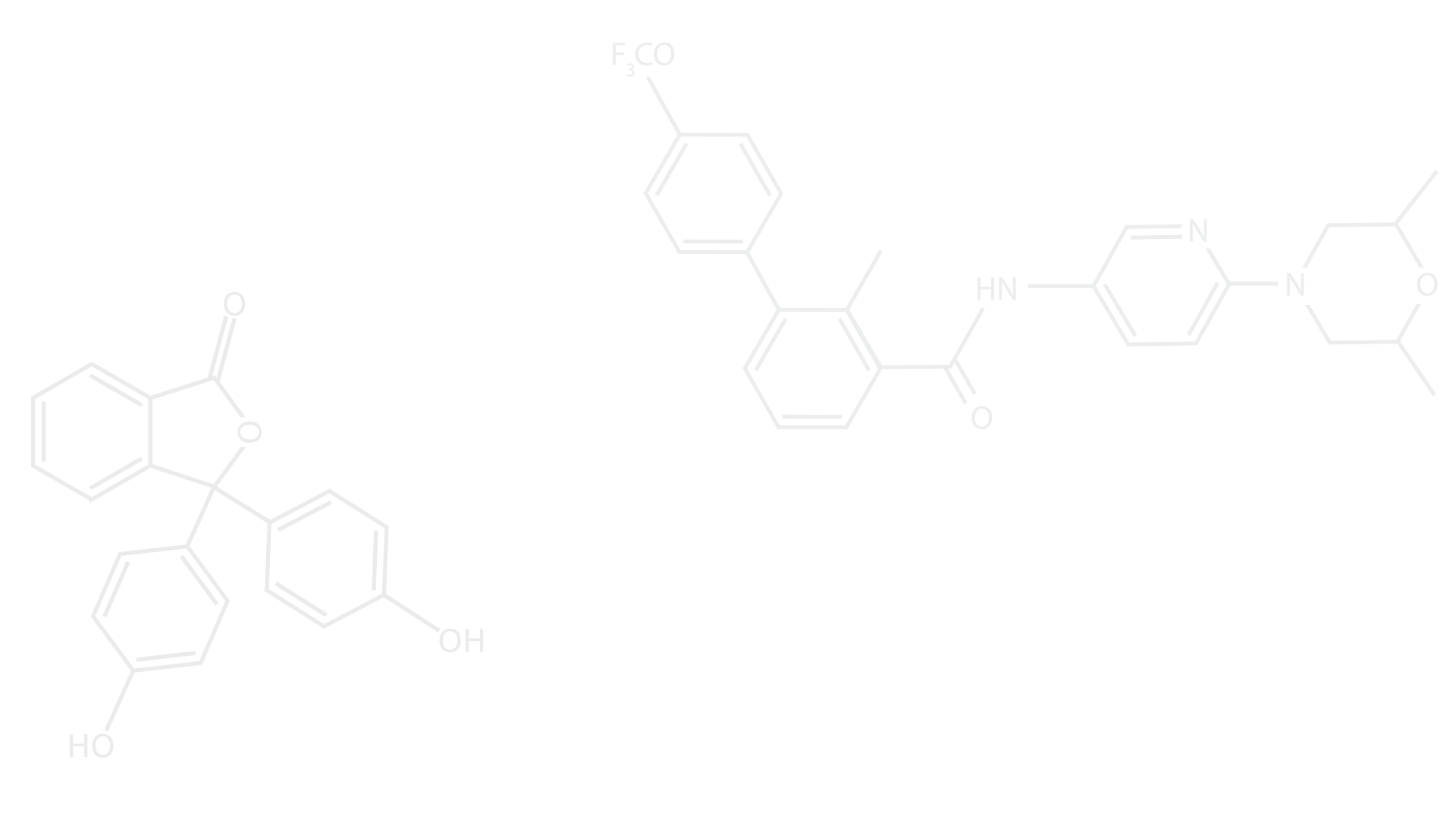
1. The wavemaker problem:
Long-time asymptotic analysis
(Steepest descent contour for the linear BBM boundary value problem)

Experimental results
2. Breathers in soliton - periodic wave interactions


3. Breather shock waves


Transport by weakly nonlinear internal gravity waves
This study investigates how internal gravity waves (IGWs) contribute to chemical mixing in the radiative zones of stars through theoretical analysis and numerical simulations. Using multiscale asymptotic analysis, we show that the net transport induced by a coherent wave packet scales with the fourth power of its amplitude, and we confirm this scaling through Dedalus direct numerical simulations (Burns, 2020). Because the transport is equally likely to be positive as negative, the transport by a random superposition of waves is expected to scale as wave amplitude to the eighth power.

Surface breaking waves in air-sea interaction
Breaking waves play a crucial role in driving mixing within the oceanic and atmospheric boundary layers, thereby modulating air–sea exchanges of momentum, heat, and freshwater that are vital to Earth’s climate system. They enable a two-way transfer of mass and energy across the air–sea interface, serving as a key mechanism in ocean–atmosphere coupling. In this study, using the Basilisk solver (Popinet, 2009), we focus on surface-breaking plunging waves and examine the physical mechanisms responsible for wave energy dissipation during breaking events.

Linear stability of superposed inviscid and viscous stagnation-point flows
We examine the stability of two-layer stagnation-point and rotating flows with differing densities and viscosities, assuming a flat interface between the layers. The stability of an inviscid two-layer rotating flow is first analyzed as an initial-value problem, revealing the presence of instability. Building on the work of Brattku & Davis (1991), who investigated the stability of stagnation-point flow over a single boundary, we then analyze the linear stability of a two-layer viscous stagnation-point flow with a similarity-solution base state under the long-wave approximation. The resulting eigenvalue problem is solved numerically, and the key properties and limiting cases of the system are discussed.